https://www.acmicpc.net/problem/2042

1. 아이디어
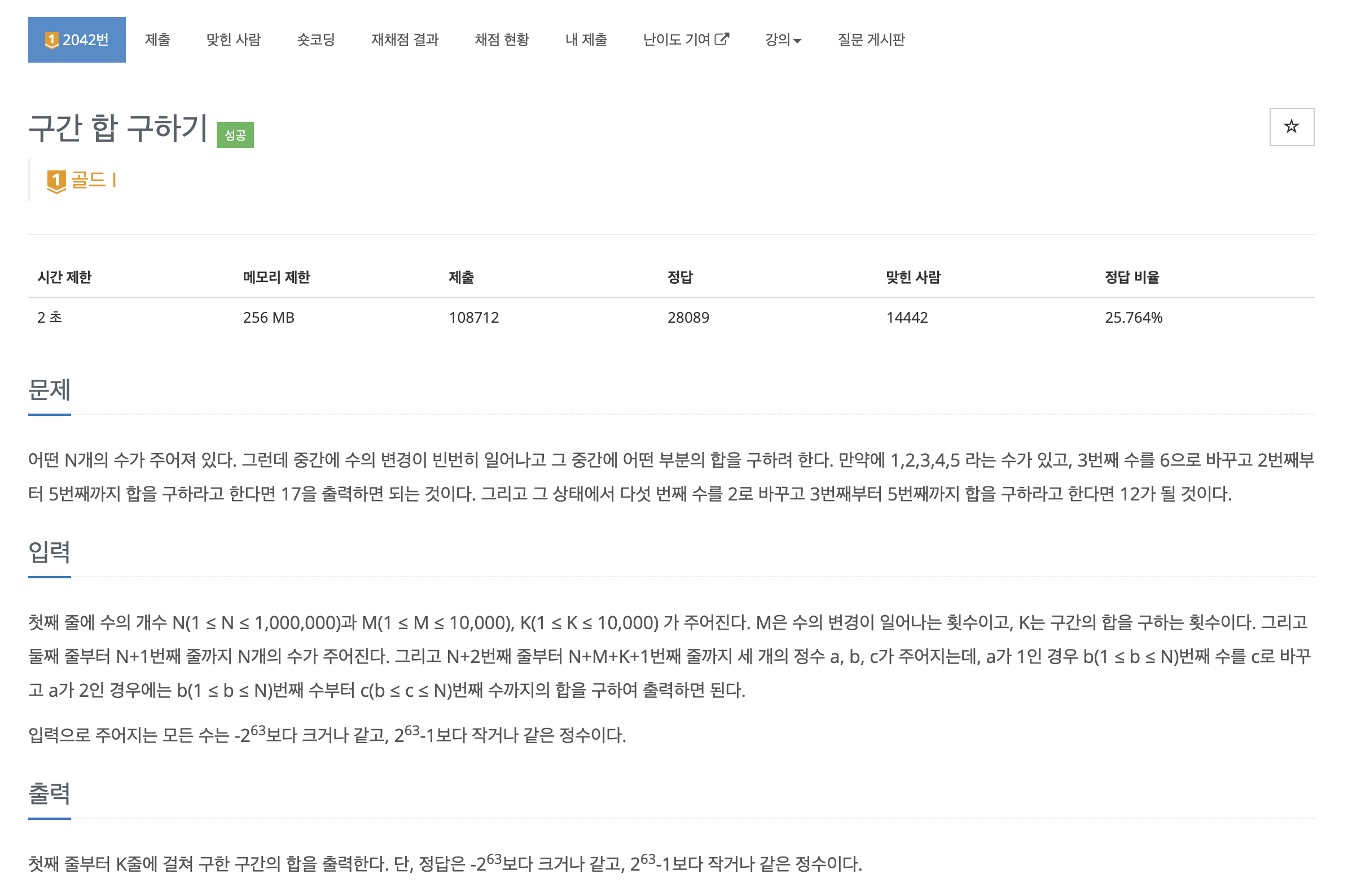
구간에 대한 합을 반복적으로 구해야하고 특정 위치의 값을 변경하는 상황도 있다는 점에서 세그먼트 트리를 활용하면 간단하게 해결할 수 있다.
2. 문제풀이
세그먼트 트리 클래스를 구현한 후 입력 값을 기반으로 세그먼트 트리를 생성해서 반복문으로 쿼리를 처리하는 방식으로 구현했다.
세그먼트 트리는 구간 합을 구해야하므로 자식 노드의 합을 저장하도록 초기화 및 쿼리를 짰다. 쿼리에서 구간이 벗어나는 경우 포함하지 않는다는 의미로 0을 반환해서 한다.
3. 코드
import java.io.*;
import java.util.*;
public class Main {
private static class SegmentTree {
private final int N;
private final long[] tree;
public SegmentTree(long[] arr) {
this.N = arr.length;
this.tree = new long[4 * N];
init(arr, 1, 0, N - 1);
}
private long init(long[] arr, int node, int start, int end) {
if (start == end) return tree[node] = arr[start];
int mid = (start + end) / 2;
int leftChild = 2 * node;
int rightChild = 2 * node + 1;
return tree[node] = init(arr, leftChild, start, mid) + init(arr, rightChild, mid + 1, end);
}
private long query(int left, int right) {
return query(1, 0, N - 1, left, right);
}
private long query(int node, int start, int end, int left, int right) {
if (left > end || right < start) return 0;
if (left <= start && end <= right) return tree[node];
int mid = (start + end) / 2;
int leftChild = 2 * node;
int rightChild = 2 * node + 1;
return query(leftChild, start, mid, left, right) + query(rightChild, mid + 1, end, left, right);
}
private void update(int idx, long value) {
update(1, 0, N - 1, idx, value);
}
private void update(int node, int start, int end, int idx, long value) {
if (start == end) {
tree[node] = value;
return;
}
int mid = (start + end) / 2;
int leftChild = 2 * node;
int rightChild = 2 * node + 1;
if (idx <= mid) {
update(leftChild, start, mid, idx, value);
} else {
update(rightChild, mid + 1, end, idx, value);
}
tree[node] = tree[leftChild] + tree[rightChild];
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb = new StringBuilder();
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
long[] arr = new long[N];
for (int i = 0; i < N; i++) {
arr[i] = Long.parseLong(br.readLine());
}
SegmentTree tree = new SegmentTree(arr);
for (int i = 0; i < M + K; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
long c = Long.parseLong(st.nextToken());
if (a == 1) tree.update(b - 1, c);
else sb.append(tree.query(b - 1, (int) c - 1)).append("\n");
}
bw.write(sb.toString());
bw.flush();
}
}4. 후기

'코딩테스트 준비 > 백준' 카테고리의 다른 글
| [백준] 11505번 - 구간 곱 구하기 [Java] (0) | 2025.01.14 |
|---|---|
| [백준] 1275번 - 커피숍2 [Java] (0) | 2025.01.14 |
| [백준] 12348번 - 분해합 2 [Java] (0) | 2025.01.14 |
| [백준] 2231번 - 분해합 [Java] (0) | 2025.01.14 |
| [백준] 15482번 - 한글 LCS [Java] (0) | 2025.01.14 |



